AlphaVerus

Bootstrapping Formally Verified Code Generation through Self-Improving Translation and Treefinement

Pranjal Aggarwal1, Bryan Parno1, Sean Welleck1

1Carnegie Mellon University


Paper Code Results AlphaVerus in Action Contact

TLDR: AlphaVerus leverages self-improvement and formal verification to generate provably correct code. It translates from known verified sources, refines code via tree search, and prevents reward hacking with a critique step, achieving robust verified code generation in real-world languages like Rust (Verus).

Why Formally Verified Code Generation?

While LLMs have shown great promise in generating code, ensuring the correctness of generated code remains a significant challenge. Bugs and vulnerabilities can have serious consequences. Formal verification offers mathematical guarantees of correctness but is hindered by data scarcity and proof complexity.

Introducing AlphaVerus

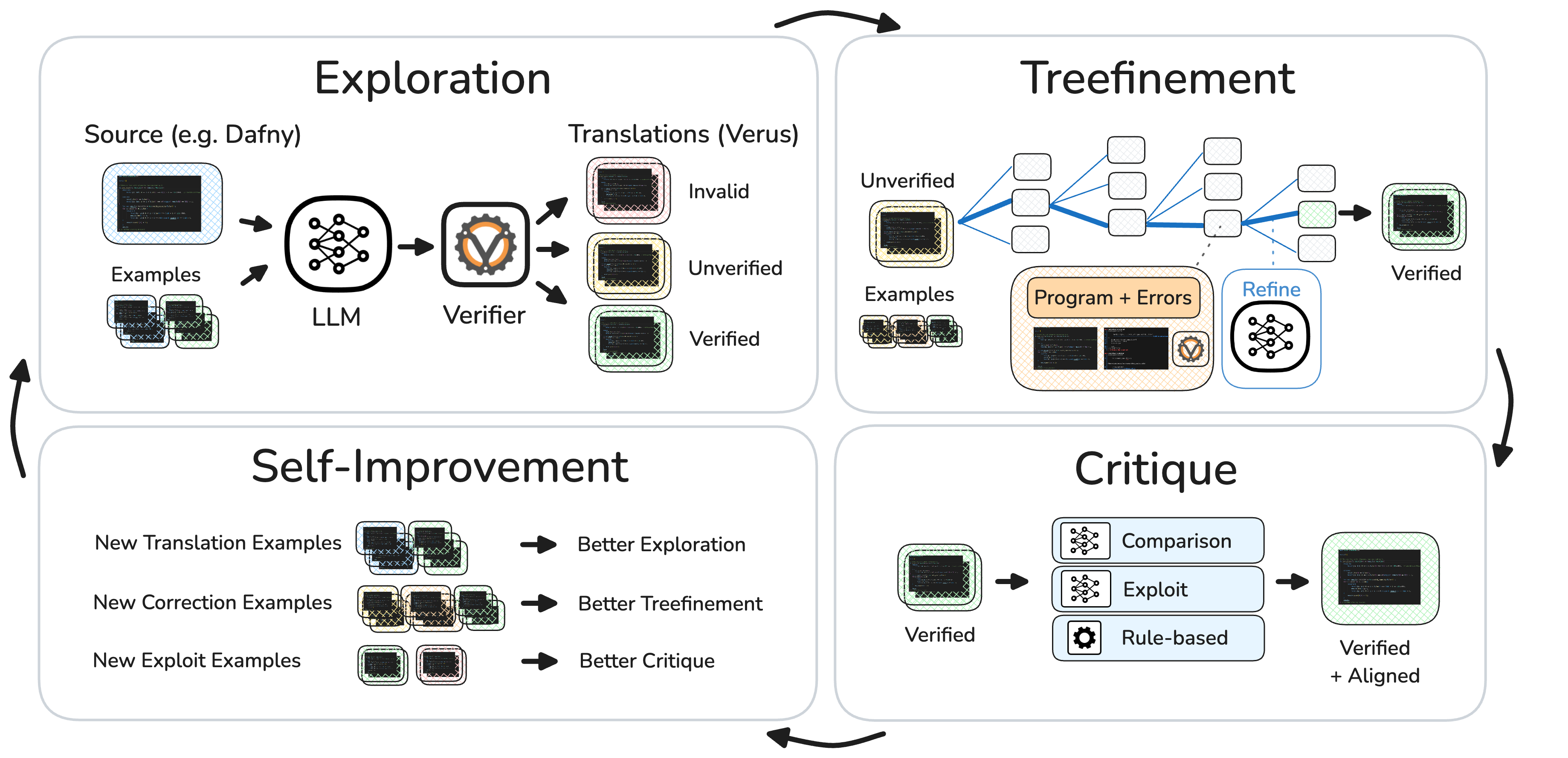
AlphaVerus Framework Diagram


AlphaVerus is a self-improving framework that bootstraps formally verified code generation by translating programs from a higher-resource language and leveraging feedback from a verifier. It operates in three phases:

  • Exploration: Translates programs from a source language.
  • Treefinement: Refines translations using a novel tree search algorithm.
  • Critique: Filters misaligned specifications to prevent reward hacking.

Key Highlights

  • 🔑 Formal Guarantees: AlphaVerus integrates formal verification into code generation, ensuring mathematically guaranteed correctness.
  • 🚀 Self-Improvement: Iterative translation and refinement build a data collection loop that continuously improves generation quality without human intervention.
  • 🌳 Treefinement Algorithm: A novel tree-search-based refinement process fixes verification errors efficiently, surpassing linear refinement methods.
  • 🛡 Preventing Reward Hacking: A critique step filters out trivial or misaligned specs, maintaining the integrity of the training cycle, which is crucial for the self-improvement loop.
  • 📊 Strong Results: Achieves state-of-the-art verified code generation performance on HumanEval-Verus and MBPP-Verus benchmarks.

Interesting Contributions

Self-Improving Framework

AlphaVerus iteratively improves code generation by learning from translations and verifier feedback, without human intervention or model fine-tuning. This self-improvement allows it to handle increasingly complex verifiable code generation tasks.

Self-Improvement Process

Treefinement Algorithm

The novel Treefinement algorithm performs a tree search over program refinements using verifier feedback. It outperforms traditional linear refinement methods by prioritizing promising paths and efficiently finding verified programs.

Treefinement Algorithm

Preventing Reward Hacking

AlphaVerus employs critique models to filter out misaligned specifications and trivial solutions that pass verification but don't fulfill the intended functionality, ensuring the correctness and reliability of generated code.

Preventing Reward Hacking

AlphaVerus in Action

Explore examples generated by AlphaVerus demonstrating specifications, code, and proofs.

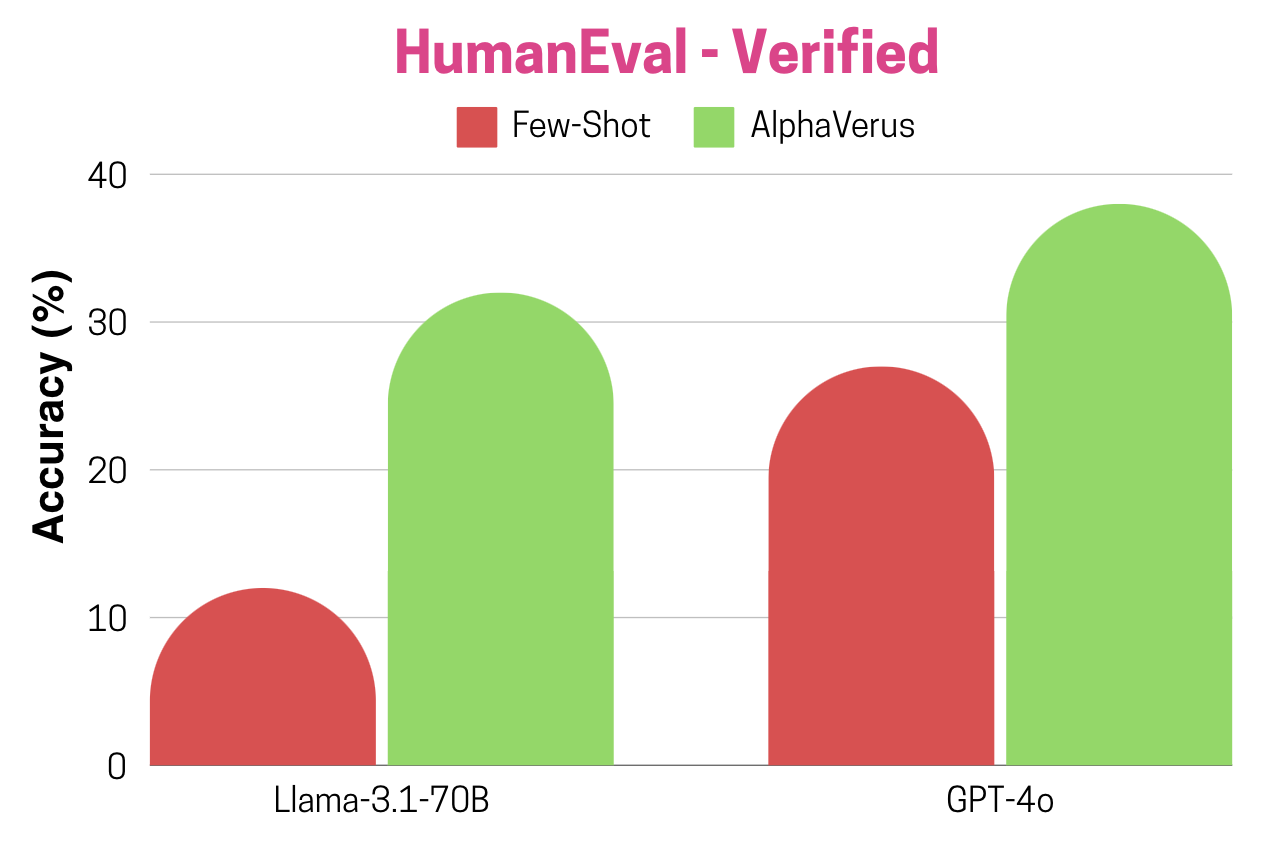
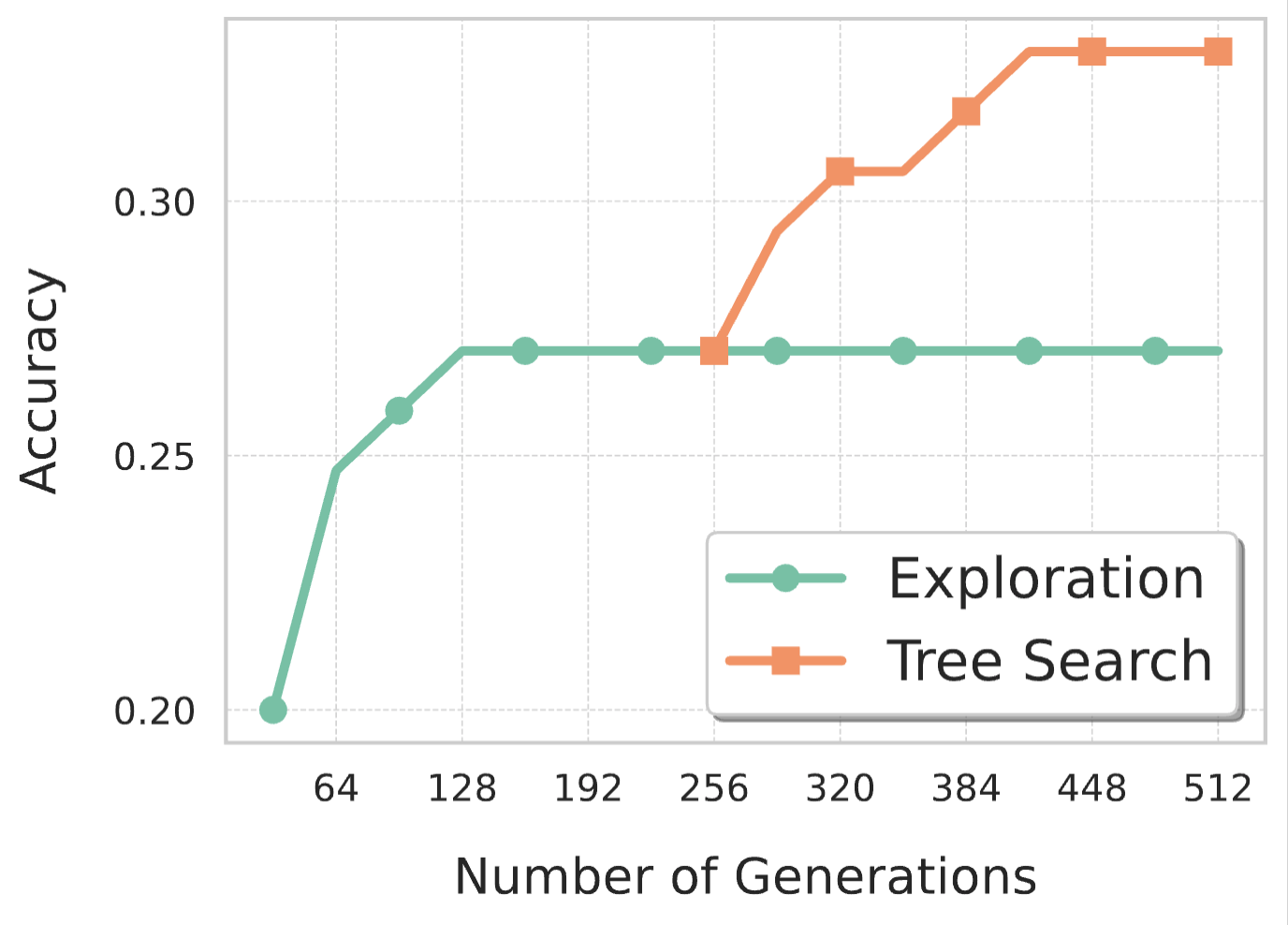
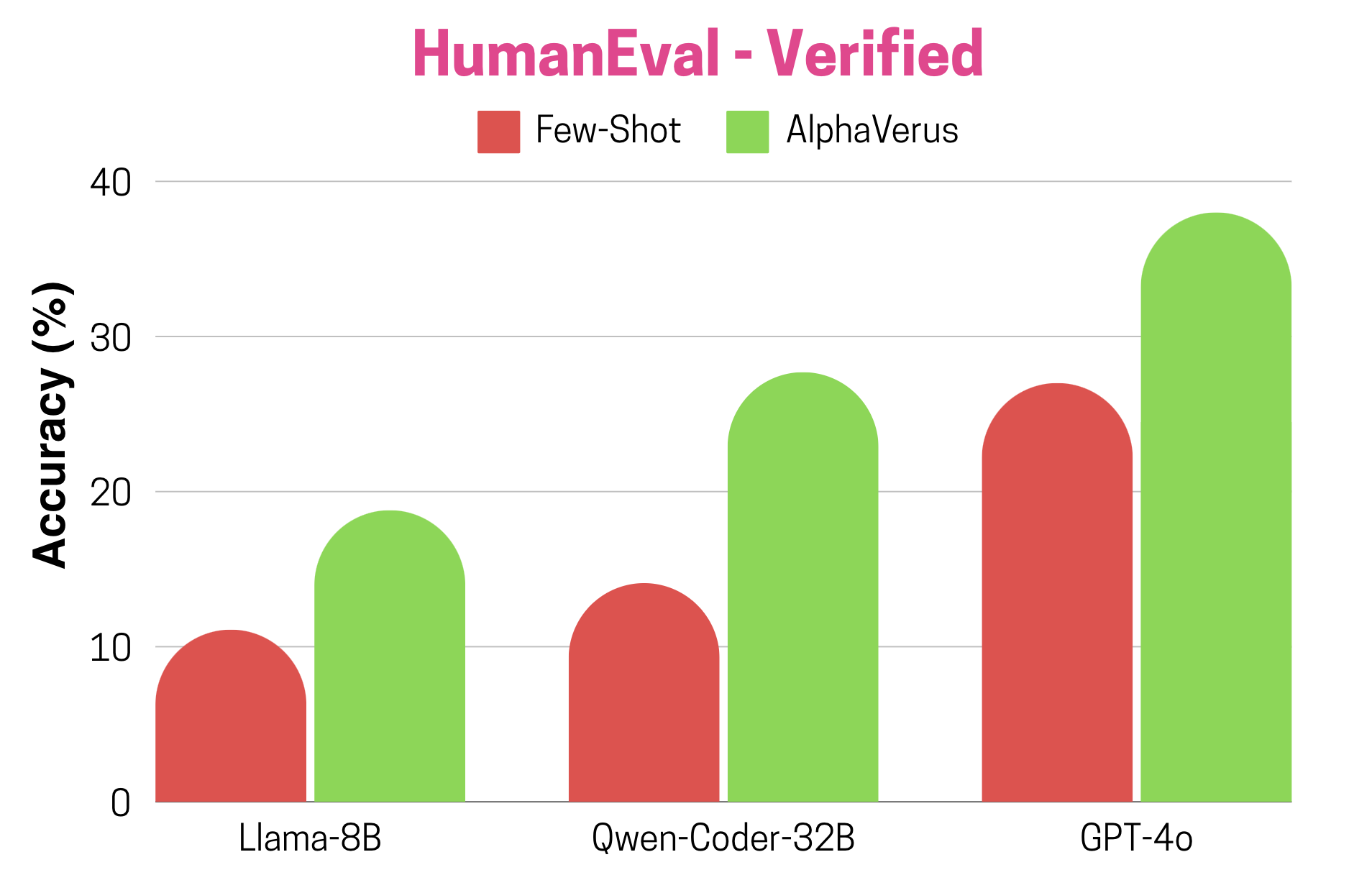
Multi-Function Verification: Prime Number Functions

Demonstrates verification of multiple related functions with helper functions

Stage 1: Prime Number Checker Specification

spec fn spec_prime_helper(num: int, limit: int) -> bool {
    forall|j: int| 2 <= j < limit ==> (#[trigger] (num % j)) != 0
}

spec fn spec_prime(num: int) -> bool {
    spec_prime_helper(num, num)
}

fn is_prime(num: u32) -> (result: bool)
    requires
        num >= 2,
    ensures
        result <==> spec_prime(num as int),

Stage 1: Code + Proof

let mut i = 2;
let mut result = true;
while i < num
    invariant
        2 <= i <= num,
        result <==> spec_prime_helper(num as int, i as int),
{
    if num % i == 0 {
        result = false;
    }
    i += 1;
}
result

Stage 2: Largest Prime Factor Specification

fn largest_prime_factor(n: u32) -> (largest: u32)
    requires
        n >= 2,
    ensures
        1 <= largest <= n,
        spec_prime(largest as int),
        n % largest == 0,
        forall|p| 0 <= p < n && spec_prime(p) && n as int % p == 0 ==> p <= largest

Stage 2: Code + Proof

let mut largest = 1;
let mut i = 2;
while i < n
    invariant
        2 <= i <= n,
        1 <= largest <= i,
        spec_prime(largest as int),
        i <= largest ==> spec_prime(i as int),
        largest <= n,
        n % largest == 0,
        forall|p| 0 <= p < i && spec_prime(p) && n as int % p == 0 ==> p <= largest,
{
    if is_prime(i) && n % i == 0 {
        largest = i;
    }
    i += 1;
}
assert(1 <= largest && largest <= n);
assert(spec_prime(largest as int));
assert(n % largest == 0);
assert(forall|p| 0 <= p < n && spec_prime(p) && n as int % p == 0 ==> p <= largest);
largest

Advanced Proof: String Manipulation Lemma

Shows complex string reasoning with detailed verification steps

Specification

proof fn lemma_step_subrange(substring: Seq, string: Seq)
    requires
        substring.len() > 0,
        string.len() >= substring.len(),
    ensures
        (substring[0] == string.subrange(0, substring.len() as int)[0] && (substring.skip(1)
            =~= string.skip(1).subrange(0, substring.skip(1).len() as int))) ==> (substring
            =~= string.subrange(0, substring.len() as int)),
    decreases substring.len(),

Code + Proof (Generated by AlphaVerus)

let m = substring.len();
let n = string.len();
assert(m > 0);
assert(m <= n);
let h = string.subrange(0, m as int);
assert(h.len() == m);
assert(substring.len() == h.len());
if substring[0] == h[0] {
    let k = substring.skip(1).len();
    assert(k == h.skip(1).len());
    let g = string.skip(1).subrange(0, k as int);
    assert(g.len() == k);
    assert(k == substring.len() - 1);
    assert(k == h.len() - 1);
    if m > 1 {
        if substring.skip(1) =~= g {
            assert(substring[0] == h[0]);
            assert(substring.len() == g.len() + 1);
            assert(substring.len() == h.len());
            assert(forall|i: nat| 0 <= i && i < m ==> substring[i as int] == h[i as int]) by {
                assert(substring[0] == h[0]);
                assert(substring.skip(1) =~= g);
                assert(forall|i: nat| 1 <= i && i < m ==> substring[i as int] == g[i as int - 1]);
                assert(substring =~= h);
            }
            assert(substring =~= h);
        } else {
            assert(!(substring =~= h));
        }
    } else {
        assert(substring =~= h);
    }
} else {
    assert(!(substring =~= h));
}

Translation Example: Dafny to Verus

All Code is AlphaVerus-Generated

Translation of Recursive Implementation

use vstd::prelude::*;

verus! {
fn search_recursive(a: &Vec, i: usize, j: usize, x: i32) -> (k: i32)
    requires
        0 <= i && i <= j && j <= a.len(),
        j - i < 100000,
        j <= i32::MAX as usize,
    ensures
        i <= k && k < j || k == -1,
        k != -1 ==> a[k as int] == x,
        k != -1 ==> forall|r: nat| k < r && r < j ==> a[r as int] != x,
        k == -1 ==> forall|r: nat| i <= r && r < j ==> a[r as int] != x,
    decreases
        j - i,
{
    if j == i {
        -1
    } else if a[j - 1] == x {
        assert(j - 1 <= i32::MAX as usize);
        if j - 1 <= i32::MAX as usize {
            (j - 1) as i32
        } else {
            -1
        }
    } else {
        search_recursive(a, i, j - 1, x)
    }
}

Translation of Iterative Implementation

fn search_loop(a: &Vec, i: usize, j: usize, x: i32) -> (k: i32)
    requires
        0 <= i && i <= j && j <= a.len(),
        j - i < 100000,
        j <= i32::MAX as usize,
    ensures
        i <= k && k < j || k == -1,
        k != -1 ==> a[k as int] == x,
        k != -1 ==> forall|r: nat| k < r && r < j ==> a[r as int] != x,
        k == -1 ==> forall|r: nat| i <= r && r < j ==> a[r as int] != x,
{
    if i == j {
        return -1;
    }
    let mut t: usize = j;
    while t > i
        invariant
            0 <= i <= t && t <= j,
            t <= a.len(),
            forall|p: nat| t <= p && p < j ==> a[p as int] != x,
            t <= i32::MAX as usize,
        decreases
            t,
    {
        assert(t <= a.len());
        if a[t - 1] == x {
            if t - 1 <= i32::MAX as usize {
                return (t - 1) as i32;
            } else {
                return -1;
            }
        } else {
            assert(t > i);
            t = t - 1;
        }
    }
    -1
}

Performance Highlights

State-of-the-Art Results

AlphaVerus achieves significant improvements in generating formally verified code, outperforming existing methods including GPT-4. Our framework reaches 38% success rate on HumanEval-Verified, setting a new benchmark for verified code generation.

Performance Chart

Scaling Inference Compute

AlphaVerus's Exploration Stage and Treefinement algorithm efficiently scales with additional compute, showing consistent improvements in verification success rates. This demonstrates the framework's ability to leverage computational resources effectively for better results.

Scaling Inference Compute

No-Finetuning Model Transfer

AlphaVerus's collected exemplars can improve any new model's performance without fine-tuning, demonstrating strong transfer capabilities. This makes our framework a valuable tool for improving verified code generation across different models.

No Finetuning Model Transfer

BibTeX

@misc{aggarwal2024alphaverusbootstrappingformallyverified,
      title={AlphaVerus: Bootstrapping Formally Verified Code Generation through Self-Improving Translation and Treefinement}, 
      author={Pranjal Aggarwal and Bryan Parno and Sean Welleck},
      year={2024},
      eprint={2412.06176},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      url={https://arxiv.org/abs/2412.06176}, 
}